跳转至

Index

从RNN说起

RNN的输出：

\[ \hat{\boldsymbol y} = \mathrm{softmax}\left(\boldsymbol{U}\boldsymbol{h}^{(t)} + \boldsymbol b_2 \right) \in \mathbf{R}^{|V|} \]

RNN的隐藏状态：

\[ \boldsymbol{h}^{(t)} = \sigma\left(\boldsymbol{W}_h\boldsymbol{h}^{(t-1)} + \boldsymbol{W}_e \boldsymbol{e}^{(t)} + \boldsymbol{b}_1 \right) \]

其中\(\boldsymbol{h}^{(0)}\)是初始隐藏状态，词嵌入

\[ \boldsymbol{e}^{(t)} = \boldsymbol{E}\boldsymbol{x}^{(t)} \]

词（one-hot向量）\(\boldsymbol{x}^{(t)} \in \mathbf{R}^{|V|}\)

反向传播的过程：

\[ \frac{\partial J^{(t)}}{\partial \boldsymbol{W}_\boldsymbol{h}} = \left.\sum_{i=1}^{t} \frac{\partial J^{(t)}}{\partial \boldsymbol{W}_{\boldsymbol{h}}}\right|_{(i)} \]

此策略被称为Backpropagation through time1。

评估语言模型的最基本方案是\(\mathrm{perplexity}\)，

\[ \begin{aligned} \text { perplexity } &=\prod_{t=1}^{T}\left(\frac{1}{P_{\mathrm{LM}}\left(\boldsymbol{x}^{(t+1)} \mid \boldsymbol{x}^{(t)}, \ldots, \boldsymbol{x}^{(1)}\right)}\right)^{1 / T} \\ &=\prod_{t=1}^{T}\left(\frac{1}{\hat{\boldsymbol{y}}_{\boldsymbol{x}_{t+1}}^{(t)}}\right)^{1 / T}=\exp \left(\frac{1}{T} \sum_{t=1}^{T}-\log \hat{\boldsymbol{y}}_{\boldsymbol{x}_{t+1}}^{(t)}\right)\\&=\exp (J(\theta)) \end{aligned} \]

也就是交叉熵的指数。

但是，RNN需要将一个序列读入，全部计算梯度后才能反向传播，容易引起梯度消失和梯度爆炸。有人提出了梯度裁剪和 truncated backpropagation through time，但是都没有从根本上解决问题。

LSTM

\[ \begin{aligned} \boldsymbol{f}^{(t)} &=\sigma\left(\boldsymbol{W}_{f} \boldsymbol{h}^{(t-1)}+\boldsymbol{U}_{f} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{f}\right) \\ \boldsymbol{i}^{(t)} &=\sigma\left(\boldsymbol{W}_{i} \boldsymbol{h}^{(t-1)}+\boldsymbol{U}_{i} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{i}\right) \\ \boldsymbol{o}^{(t)} &=\sigma\left(\boldsymbol{W}_{o} \boldsymbol{h}^{(t-1)}+\boldsymbol{U}_{o} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{o}\right) \\ \tilde{\boldsymbol{c}}^{(t)} &=\tanh \left(\boldsymbol{W}_{c} \boldsymbol{h}^{(t-1)}+\boldsymbol{U}_{c} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{c}\right) \\ \boldsymbol{c}^{(t)} &=\boldsymbol{f}^{(t)} \circ \boldsymbol{c}^{(t-1)}+\boldsymbol{i}^{(t)} \circ \tilde{\boldsymbol{c}}^{(t)} \\ \boldsymbol{h}^{(t)} &=\boldsymbol{o}^{(t)} \circ \tanh \boldsymbol{c}^{(t)} \end{aligned} \]

LSTM 有三个门、三个状态：

  • \(\boldsymbol f\) 被称为 forget gate，决定对 cell 的哪些状态“记住”哪些进行“遗忘”；
  • \(\boldsymbol i\) 被称为“输入门”，用于决定输入\(\boldsymbol x\)的哪些部分会进入 cell；

  • \(\boldsymbol o\) 被称为“输出门”，用于决定 cell 的哪部分会影响输出；

  • \(\tilde{\boldsymbol{c}}^{(t)}\) 为由\(x\)计算得到的 cell 的新状态

  • \(\boldsymbol c^{(t)}\) 为 cell 下一时刻的状态
  • \(\boldsymbol h^{(t)}\) 为输出状态

GRU

\[ \begin{aligned} &\boldsymbol{u}^{(t)}=\sigma\left(\boldsymbol{W}_{u} \boldsymbol{h}^{(t-1)}+\boldsymbol{U}_{u} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{u}\right) \\ &\boldsymbol{r}^{(t)}=\sigma\left(\boldsymbol{W}_{r} \boldsymbol{h}^{(t-1)}+\boldsymbol{U}_{r} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{r}\right) \\ &\tilde{\boldsymbol{h}}^{(t)}=\tanh \left(\boldsymbol{W}_{h}\left(\boldsymbol{r}^{(t)} \circ \boldsymbol{h}^{(t-1)}\right)+\boldsymbol{U}_{h} \boldsymbol{x}^{(t)}+\boldsymbol{b}_{h}\right) \\ &\boldsymbol{h}^{(t)}=\left(1-\boldsymbol{u}^{(t)}\right) \circ \boldsymbol{h}^{(t-1)}+\boldsymbol{u}^{(t)} \circ \tilde{\boldsymbol{h}}^{(t)} \end{aligned} \]

与 LSTM 相比，GRU 没有 cell 的概念，而是使用 update gate 和 reset gate 来控制对 hidden state 的更新。

LSTM vs. GRU

LSTM 和 GRU 是最常用的 RNN 变种，在通常情况下，LSTM 是不错的选择，但 GRU 有更少的参数量和更快的训练速度。

还有个很有意思的事实是，LSTM 比 GRU 更容易学会计数2。

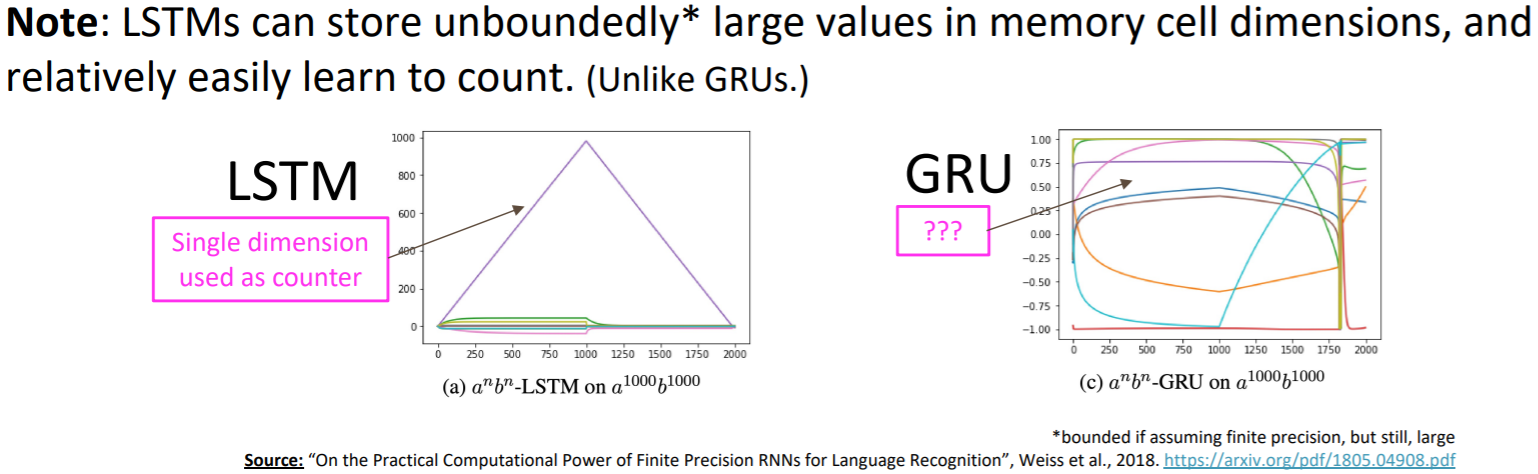image-20220125201724116{loading=lazy}

实现

最简 LSTM 实现，来自3。

import random

import numpy as np
import math

def sigmoid(x):
    return 1. / (1 + np.exp(-x))

def sigmoid_derivative(values):
    return values*(1-values)

def tanh_derivative(values):
    return 1. - values ** 2

# createst uniform random array w/ values in [a,b) and shape args
def rand_arr(a, b, *args):
    np.random.seed(0)
    return np.random.rand(*args) * (b - a) + a

class LstmParam:
    def __init__(self, mem_cell_ct, x_dim):
        self.mem_cell_ct = mem_cell_ct
        self.x_dim = x_dim
        concat_len = x_dim + mem_cell_ct
        # weight matrices
        self.wg = rand_arr(-0.1, 0.1, mem_cell_ct, concat_len)
        self.wi = rand_arr(-0.1, 0.1, mem_cell_ct, concat_len)
        self.wf = rand_arr(-0.1, 0.1, mem_cell_ct, concat_len)
        self.wo = rand_arr(-0.1, 0.1, mem_cell_ct, concat_len)
        # bias terms
        self.bg = rand_arr(-0.1, 0.1, mem_cell_ct)
        self.bi = rand_arr(-0.1, 0.1, mem_cell_ct)
        self.bf = rand_arr(-0.1, 0.1, mem_cell_ct)
        self.bo = rand_arr(-0.1, 0.1, mem_cell_ct)
        # diffs (derivative of loss function w.r.t. all parameters)
        self.wg_diff = np.zeros((mem_cell_ct, concat_len))
        self.wi_diff = np.zeros((mem_cell_ct, concat_len))
        self.wf_diff = np.zeros((mem_cell_ct, concat_len))
        self.wo_diff = np.zeros((mem_cell_ct, concat_len))
        self.bg_diff = np.zeros(mem_cell_ct)
        self.bi_diff = np.zeros(mem_cell_ct)
        self.bf_diff = np.zeros(mem_cell_ct)
        self.bo_diff = np.zeros(mem_cell_ct)

    def apply_diff(self, lr = 1):
        self.wg -= lr * self.wg_diff
        self.wi -= lr * self.wi_diff
        self.wf -= lr * self.wf_diff
        self.wo -= lr * self.wo_diff
        self.bg -= lr * self.bg_diff
        self.bi -= lr * self.bi_diff
        self.bf -= lr * self.bf_diff
        self.bo -= lr * self.bo_diff
        # reset diffs to zero
        self.wg_diff = np.zeros_like(self.wg)
        self.wi_diff = np.zeros_like(self.wi)
        self.wf_diff = np.zeros_like(self.wf)
        self.wo_diff = np.zeros_like(self.wo)
        self.bg_diff = np.zeros_like(self.bg)
        self.bi_diff = np.zeros_like(self.bi)
        self.bf_diff = np.zeros_like(self.bf)
        self.bo_diff = np.zeros_like(self.bo)

class LstmState:
    def __init__(self, mem_cell_ct, x_dim):
        self.g = np.zeros(mem_cell_ct)
        self.i = np.zeros(mem_cell_ct)
        self.f = np.zeros(mem_cell_ct)
        self.o = np.zeros(mem_cell_ct)
        self.s = np.zeros(mem_cell_ct)
        self.h = np.zeros(mem_cell_ct)
        self.bottom_diff_h = np.zeros_like(self.h)
        self.bottom_diff_s = np.zeros_like(self.s)

class LstmNode:
    def __init__(self, lstm_param, lstm_state):
        # store reference to parameters and to activations
        self.state = lstm_state
        self.param = lstm_param
        # non-recurrent input concatenated with recurrent input
        self.xc = None

    def bottom_data_is(self, x, s_prev = None, h_prev = None):
        # if this is the first lstm node in the network
        if s_prev is None: s_prev = np.zeros_like(self.state.s)
        if h_prev is None: h_prev = np.zeros_like(self.state.h)
        # save data for use in backprop
        self.s_prev = s_prev
        self.h_prev = h_prev

        # concatenate x(t) and h(t-1)
        xc = np.hstack((x,  h_prev))
        self.state.g = np.tanh(np.dot(self.param.wg, xc) + self.param.bg)
        self.state.i = sigmoid(np.dot(self.param.wi, xc) + self.param.bi)
        self.state.f = sigmoid(np.dot(self.param.wf, xc) + self.param.bf)
        self.state.o = sigmoid(np.dot(self.param.wo, xc) + self.param.bo)
        self.state.s = self.state.g * self.state.i + s_prev * self.state.f
        self.state.h = self.state.s * self.state.o

        self.xc = xc

    def top_diff_is(self, top_diff_h, top_diff_s):
        # notice that top_diff_s is carried along the constant error carousel
        ds = self.state.o * top_diff_h + top_diff_s
        do = self.state.s * top_diff_h
        di = self.state.g * ds
        dg = self.state.i * ds
        df = self.s_prev * ds

        # diffs w.r.t. vector inside sigma / tanh function
        di_input = sigmoid_derivative(self.state.i) * di
        df_input = sigmoid_derivative(self.state.f) * df
        do_input = sigmoid_derivative(self.state.o) * do
        dg_input = tanh_derivative(self.state.g) * dg

        # diffs w.r.t. inputs
        self.param.wi_diff += np.outer(di_input, self.xc)
        self.param.wf_diff += np.outer(df_input, self.xc)
        self.param.wo_diff += np.outer(do_input, self.xc)
        self.param.wg_diff += np.outer(dg_input, self.xc)
        self.param.bi_diff += di_input
        self.param.bf_diff += df_input
        self.param.bo_diff += do_input
        self.param.bg_diff += dg_input

        # compute bottom diff
        dxc = np.zeros_like(self.xc)
        dxc += np.dot(self.param.wi.T, di_input)
        dxc += np.dot(self.param.wf.T, df_input)
        dxc += np.dot(self.param.wo.T, do_input)
        dxc += np.dot(self.param.wg.T, dg_input)

        # save bottom diffs
        self.state.bottom_diff_s = ds * self.state.f
        self.state.bottom_diff_h = dxc[self.param.x_dim:]

class LstmNetwork():
    def __init__(self, lstm_param):
        self.lstm_param = lstm_param
        self.lstm_node_list = []
        # input sequence
        self.x_list = []

    def y_list_is(self, y_list, loss_layer):
        """
        Updates diffs by setting target sequence
        with corresponding loss layer.
        Will *NOT* update parameters.  To update parameters,
        call self.lstm_param.apply_diff()
        """
        assert len(y_list) == len(self.x_list)
        idx = len(self.x_list) - 1
        # first node only gets diffs from label ...
        loss = loss_layer.loss(self.lstm_node_list[idx].state.h, y_list[idx])
        diff_h = loss_layer.bottom_diff(self.lstm_node_list[idx].state.h, y_list[idx])
        # here s is not affecting loss due to h(t+1), hence we set equal to zero
        diff_s = np.zeros(self.lstm_param.mem_cell_ct)
        self.lstm_node_list[idx].top_diff_is(diff_h, diff_s)
        idx -= 1

        ### ... following nodes also get diffs from next nodes, hence we add diffs to diff_h
        ### we also propagate error along constant error carousel using diff_s
        while idx >= 0:
            loss += loss_layer.loss(self.lstm_node_list[idx].state.h, y_list[idx])
            diff_h = loss_layer.bottom_diff(self.lstm_node_list[idx].state.h, y_list[idx])
            diff_h += self.lstm_node_list[idx + 1].state.bottom_diff_h
            diff_s = self.lstm_node_list[idx + 1].state.bottom_diff_s
            self.lstm_node_list[idx].top_diff_is(diff_h, diff_s)
            idx -= 1

        return loss

    def x_list_clear(self):
        self.x_list = []

    def x_list_add(self, x):
        self.x_list.append(x)
        if len(self.x_list) > len(self.lstm_node_list):
            # need to add new lstm node, create new state mem
            lstm_state = LstmState(self.lstm_param.mem_cell_ct, self.lstm_param.x_dim)
            self.lstm_node_list.append(LstmNode(self.lstm_param, lstm_state))

        # get index of most recent x input
        idx = len(self.x_list) - 1
        if idx == 0:
            # no recurrent inputs yet
            self.lstm_node_list[idx].bottom_data_is(x)
        else:
            s_prev = self.lstm_node_list[idx - 1].state.s
            h_prev = self.lstm_node_list[idx - 1].state.h
            self.lstm_node_list[idx].bottom_data_is(x, s_prev, h_prev)

  1. Werbos, P.G., 1988, Neural Networks 1, and others ↩

  2. http://web.stanford.edu/class/cs224n/slides/cs224n-2022-lecture06-fancy-rnn.pdf ↩

  3. https://github.com/nicodjimenez https://nicodjimenez.github.io/2014/08/08/lstm.html ↩