2022-05-29-笛卡尔树&Treap¶
| multiset | Efficient Solutions, UVa11020 | 提高 | https://www.luogu.com.cn/problem/UVA11020 |
|---|---|---|---|
| 笛卡尔树 | POJ1785 Binary Search Heap Construction | 提高 | http://bailian.openjudge.cn/practice/1785/ |
| 笛卡尔树 | Largest Rectangle in a Histogram | 提高 | http://bailian.openjudge.cn/practice/2559/ |
| Treap | Graph and Queries, Tianjin 2010 | NOI- | https://www.luogu.com.cn/problem/UVA1479 |
| Treap | Permutation Transformer, UVa11922 | NOI- | https://www.luogu.com.cn/problem/UVA11922 |
| Treap | USACO 2014 Feb G. Airplane Boarding | NOI- | https://www.luogu.com.cn/problem/P3103 |
Efficient Solutions¶
题目描述¶

输入格式¶
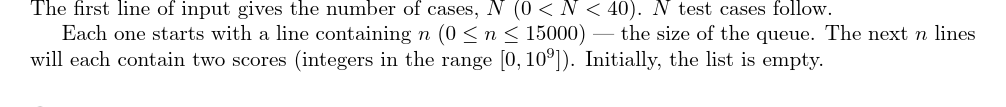
输出格式¶

样例 #1¶
样例输入 #1¶
4
1
100 200
2
100 200
101 202
2
100 200
200 100
5
11 20
20 10
20 10
100 20
1 1样例输出 #1¶
Case #1:
1
Case #2:
1
1
Case #3:
1
2
Case #4:
1
2
3
3
1Heap Construction¶
笛卡尔树是一种具有标签-优先级-对的数据结构,每一个节点的标签和优先级都是唯一的。
你的任务是构造一个包含特定节点的笛卡尔树,输出其中序遍历。
谈到笛卡尔树,很容易让人想到一种家喻户晓的结构——Treap。
没错,Treap 是笛卡尔树的一种,只不过 \(w\) 的值完全随机。Treap 也有线性的构建算法,如果提前将元素排好序,显然可以使用上述单调栈算法完成构建过程,只不过很少会这么用。
/**
* @file poj/1785/main
* @brief
* @see http://bailian.openjudge.cn/practice/solution/34585433/
* @author Ruiming Guo (guoruiming@stu.scu.edu.cn)
* @copyright 2022
* @date 5/28/2022 11:29:42
**/
#include <algorithm>
#include <cstring>
#include <iostream>
#include <utility>
#include <vector>
#define rep(i, a, b) for (int i = (a); i < (int)(b); ++i)
using namespace std;
typedef long long ll;
typedef vector<int> vi;
typedef pair<int, int> pi;
const int INF = 0x3f3f3f3f;
const ll LLINF = 0x3f3f3f3f3f3f3f3f;
const int N = 50005;
struct node {
char s[100];
int l, r, fa, idx;
bool operator<(const node &rhs) const { return strcmp(s, rhs.s) < 0; }
} p[N];
void insert(int n) {
for (int i = 1; i <= n; ++i) {
int j = i - 1;
while (p[j].idx < p[i].idx) j = p[j].fa;
p[i].l = p[j].r;
p[j].r = i;
p[i].fa = j;
}
}
void inorder(int x) {
if (x == 0) return;
putchar('(');
inorder(p[x].l);
printf("%s/%d", p[x].s, p[x].idx);
inorder(p[x].r);
putchar(')');
}
int main() {
// High rating and good luck!
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n;
while (scanf("%d", &n) != EOF && n) {
p[0].l = p[0].r = p[0].fa = 0;
for (int i = 1; i <= n; ++i) {
scanf(" %[^/]/%d", p[i].s, &p[i].idx);
p[i].l = p[i].r = p[i].fa = 0;
}
p[0].idx = INF;
sort(p + 1, p + 1 + n);
insert(n);
inorder(p[0].r);
putchar('\n');
}
return 0;
}Largest Rectangle in Histogram¶
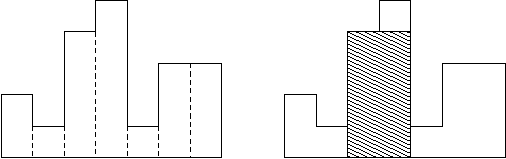 {loading=lazy}
{loading=lazy}
笛卡尔树是一种二叉树,每一个结点有一个键值二元组 \((k, w)\) 构成。
要求 \(k\) 满足**二叉搜索树的性质,\(w\) 满足堆的性质。
如果一棵笛卡尔树中的 \(k\) 互不相同,\(w\) 也互不相同,则这棵笛卡尔树是唯一的。
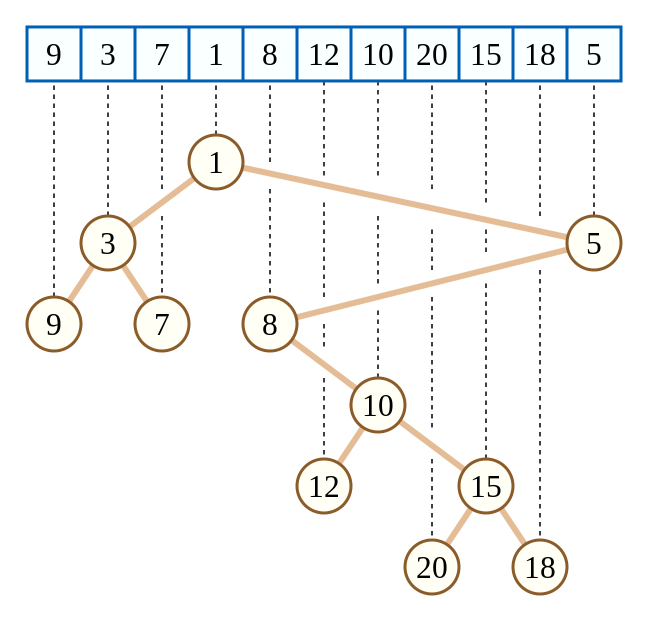 {loading=lazy}
{loading=lazy}
根据笛卡尔树的性质,对于每个矩形,以出现的下标为 \(k\),高度为 \(w\),维护一个小顶堆。
定义节点子树的大小为 \(size\),对于树上每个节点的 \(w \times size\) 就是当前节点可以作出的贡献。
维护这个贡献的最大值。
/**
* @file poj/2559/main
* @brief Largest Rectangle in a Histogram 的笛卡尔树做法
* @see
* @author Ruiming Guo (guoruiming@stu.scu.edu.cn)
* @copyright 2022
* @date 5/28/2022 17:51:24
**/
#include <iostream>
#include <stack>
#define rep(i, a, b) for (int i = (a); i < (int)(b); ++i)
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
const ll LLINF = 0x3f3f3f3f3f3f3f3f;
const int N = 1e5 + 10;
struct node {
int l, r, val;
} tree[N];
stack<int> s;
ll ans;
void insert(int x) {
while (s.size() && tree[s.top()].val > tree[x].val) s.pop();
tree[x].l = tree[s.top()].r;
tree[s.top()].r = x;
s.push(x);
}
void dfs(int k, int l, int r) {
ans = max(ans, 1LL * tree[k].val * (r - l + 1));
if (tree[k].l) dfs(tree[k].l, l, k - 1);
if (tree[k].r) dfs(tree[k].r, k + 1, r);
}
void init(int n) {
for (int i = 1; i <= n; ++i) tree[i].l = tree[i].r = 0;
while (s.size()) s.pop();
tree[0].val = -INF;
tree[0].l = tree[0].r = 0;
s.push(0);
}
int main() {
// High rating and good luck!
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int n;
while (scanf("%d", &n) != EOF && n) {
init(n);
for (int i = 1; i <= n; ++i) {
scanf("%d", &tree[i].val);
insert(i);
}
ans = 0;
dfs(0, 1, n);
printf("%lld\n", ans);
}
return 0;
}Graphs and Queries¶
有一张 \(n\) 个节点 \(m\) 条边的无向图,节点编号为 \(1 \ldots n\ (n \le 20000)\),边编号为 \(1 \ldots m\ (m \le 60000)\)。每个结点都有一个整数权值。你的任务是执行一系列操作。操作有如下三种:
- 删边:\([\mathtt D\ X]\ (1\le X \le m)\) 删除 \(\mathrm{ID}\) 为 \(X\) 的边,输入保证每条边至多被删除 \(1\) 次。
- 询问一个点连通节点的第 \(k\) 大点权:\([\mathtt Q\ X\ k]\ (1\le X\le n)\),计算与节点 \(X\) 连通的结点中(包括 \(X\) 本身),第 \(k\) 大的权值,如果不存在,返回 \(0\)。
- 修改点权:\([\mathtt C\ X\ V]\ (1\le X \le n)\) 把结点 \(X\) 的权值改为 \(V\)
操作序列结束的标志位单个字母 \([\mathtt E]\)。
对于每组数据,输出所有 \(\mathtt Q\) 指令的计算结果的平均值,输出到小数点后 6 位。
根据经验,很多数据结构不规律的合并比不规律的拆分更加容易。并且本题只需要设计离线算法,自然想到可以反过来处理。
首先读入所有操作,执行所有的 \(\mathtt D\) 操作得到最终的图;接着将边逆序插入,并在对应的时机执行 \(\mathtt Q\) 操作和 \(\mathtt C\) 操作。用一棵 Treap 维护一个连通分量中的点权,则 \(\mathtt C\) 操作对应于 Treap 中的一次修改操作,\(\mathtt Q\) 操作对应 \(k\)-th 操作,而执行 \(\mathtt D\) 操作时,如果两个端点已经是同一连通分量则无影响,否则进行启发式合并。
总时间复杂度:\(O(n\log^2n)\)
参考:https://www.luogu.com.cn/blog/andyli/solution-uva1479
呜呜呜为什么我的代码交上去就 RE。
这是洛谷的题解。
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>
using namespace std;
const int maxn = 20005, maxm = 60005, maxc = 500005;
struct Node {
Node* ch[2]; // 左右子树
int r, v, s; // 随机优先级,值,结点总数
Node(int v = 0) : v(v) {
ch[0] = ch[1] = nullptr;
r = rand();
s = 1;
}
void maintain() {
s = 1;
if (ch[0]) s += ch[0]->s;
if (ch[1]) s += ch[1]->s;
}
int cmp(int x) const { return x == v ? -1 : x < v ? 0 : 1; }
} * root[maxn];
void rotate(Node*& o, int d) {
Node* k = o->ch[d ^ 1];
o->ch[d ^ 1] = k->ch[d];
k->ch[d] = o;
o->maintain();
k->maintain();
o = k;
}
void insert(Node*& o, int x) {
if (!o)
o = new Node(x);
else {
int d = x < o->v ? 0 : 1; // 不要用cmp函数,因为可能会有相同结点
insert(o->ch[d], x);
if (o->ch[d]->r > o->r) rotate(o, d ^ 1);
}
o->maintain();
}
void remove(Node*& o, int x) {
int d = o->cmp(x);
if (d == -1) {
Node* u = o;
if (o->ch[0] && o->ch[1]) {
int d2 = o->ch[0]->r > o->ch[1]->r;
rotate(o, d2);
remove(o->ch[d2], x);
} else {
if (o->ch[0] == nullptr)
o = o->ch[1];
else
o = o->ch[0];
delete u;
}
} else
remove(o->ch[d], x);
if (o) o->maintain();
}
int kth(Node* o, int k) // 第k大的值
{
if (!o || k <= 0 || k > o->s) return 0;
int s = (o->ch[1] == nullptr ? 0 : o->ch[1]->s);
if (k == s + 1) return o->v;
if (k <= s) return kth(o->ch[1], k);
return kth(o->ch[0], k - s - 1);
}
void mergeto(Node*& src, Node*& dest) {
if (src->ch[0]) mergeto(src->ch[0], dest);
if (src->ch[1]) mergeto(src->ch[1], dest);
insert(dest, src->v);
delete src;
src = nullptr;
}
void removetree(Node*& x) {
if (x->ch[0]) removetree(x->ch[0]);
if (x->ch[1]) removetree(x->ch[1]);
delete x;
x = nullptr;
}
struct Command {
char type;
int x, p; // 根据type,p代表k或v
Command(char type = 0, int x = 0, int p = 0) : type(type), x(x), p(p) {}
} commands[maxc];
int weight[maxn], from[maxm], to[maxm], n, m;
int f[maxn], query_cnt;
bool vis[maxm];
long long query_tot;
int find(int x) { return f[x] == x ? f[x] : f[x] = find(f[x]); }
void AddEdge(int x) {
int u = find(from[x]), v = find(to[x]);
if (u != v) {
if (root[u]->s > root[v]->s) swap(u, v);
f[u] = v;
mergeto(root[u], root[v]);
}
}
void query(int x, int k) {
query_cnt++;
query_tot += kth(root[find(x)], k);
}
void change_weight(int x, int v) {
int u = find(x);
remove(root[u], weight[x]);
insert(root[u], v);
weight[x] = v;
}
int main() {
int kase = 0;
while (~scanf("%d%d", &n, &m) && n) {
for (int i = 1; i <= n; i++) scanf("%d", &weight[i]);
for (int i = 1; i <= m; i++) scanf("%d%d", &from[i], &to[i]);
memset(vis, 0, sizeof(vis));
// 读命令
int c = 0;
while (1) {
char type;
int x, p = 0, v = 0;
cin >> type;
if (type == 'E') break;
scanf("%d", &x);
if (type == 'D')
vis[x] = true;
else if (type == 'Q')
scanf("%d", &p);
else {
scanf("%d", &v);
p = weight[x];
weight[x] = v;
}
commands[c++] = Command(type, x, p);
}
// 最终的图
for (int i = 1; i <= n; i++) {
f[i] = i;
if (root[i]) removetree(root[i]);
root[i] = new Node(weight[i]);
}
for (int i = 1; i <= m; i++)
if (!vis[i]) AddEdge(i);
// 反向操作
query_tot = query_cnt = 0;
for (int i = c - 1; i >= 0; i--) {
if (commands[i].type == 'D')
AddEdge(commands[i].x);
else if (commands[i].type == 'Q')
query(commands[i].x, commands[i].p);
else
change_weight(commands[i].x, commands[i].p);
}
printf("Case %d: %.6lf\n", ++kase, query_tot * 1.0 / query_cnt);
}
return 0;
}