Attention

{loading=lazy}

The Attention Operation

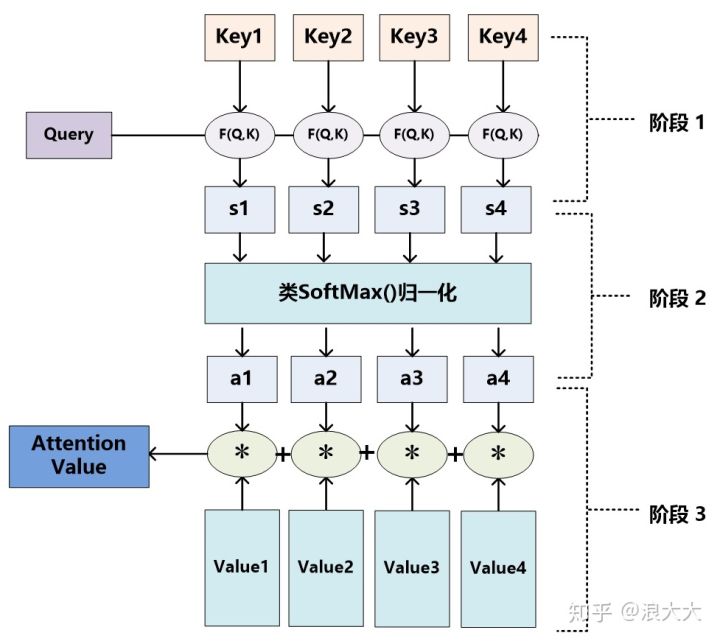
Attention is an operation that produce a result from two sequences: one sequence is \(Q\), and the other is the \((K, V)\) pair. The \((K, V)\) pair mimics the key-value pair in database retrival, and \(Q\) models the query of the retrival. Suppose we have \(n\) sample, we have inputs \(Q, K \in \mathbb{R}^{n \times d^k}\) and \(V \in \mathbb{R}^{n\times d^v}\). The attention is calculated as

\[ \operatorname{Attention}(Q, K, V) = \operatorname{softmax}\left( \frac{QK^T}{\sqrt{d^k}} \right)V, \]

Let's understand this operation step-by-step. In the softmax function, \(C =\left( \frac{QK^T}{\sqrt{d^k}}\right) \in \mathbb{R}^{n\times n}\) is the covariance between \(Q\) and \(K\). A softmax of each row cast the row vectors as probability scores. Formally, each row of \(\hat{C} = \operatorname{softmax}(C)\) gives the components to linearly combine the rows of \(V\) to form the output vector.

In self-attention, the \(Q, K, V\) are linear projections of input \(X\) by different weight matrices, i.e.,

\[ \begin{aligned} Q &= X W^Q \\ K &= X W^K \\ V &= X W^V. \end{aligned} \]

To extract more diverse information, multi-head attention is employed. The \(Q, K, V\) are projected \(h\) times using different \(W_i^{\{Q, K, V\}}\). The \(h\) \(d_v\)-dimensional output vectors are concatenanted and linearly projected to form a \(d_v\) dimensional vector.

\[ \begin{aligned} \operatorname{MultiHead}(Q, K, V) & =\operatorname{Concat}\left(\operatorname{head}_1, \ldots, \operatorname{head}_{\mathrm{h}}\right) W^O \\ \text { where head }_{\mathrm{i}} & =\operatorname{Attention}\left(Q W_i^Q, K W_i^K, V W_i^V\right) \end{aligned} \]

In cross-attention, \(Q\) and \((K, V)\) come sources. It is found to be benificial to fuse (or align) multimodal data.

Position Embedding

\[ \begin{gathered} P E_{(p o s, 2 i)}=\sin \left(p o s / 10000^{2 i / d}\right) \\ P E_{(\text {pos }, 2 i+1)}=\cos \left(\text { pos } / 10000^{2 i / d}\right) \end{gathered} \]

Where \(pos\) is the position of the word in the text sequence.

Add & Norm

Transformers solves the long-term dependency problem of the privious models, and can compute in parallel.

Attention mask

In single-directional (or causal) attention, the model predict the next work with only previous words, thus

nlp - Uni-directional Transformer VS Bi-directional BERT - Stack Overflow

The original Transformer model from Vaswani et al. is an encoder-decoder architecture. Therefore the statement "Transformer is uni-directional" is misleading.

In fact, the transformer encoder is bi-directional, which means that the self-attention can attend to tokens both on the left and right. In contrast, the decoder is uni-directional, since while generating text one token at a time, you cannot allow the decoder to attend to the right of the current token. The transformer decoder constrains the self-attention by masking the tokens to the right.

BERT uses the transformer encoder architecture and can therefore attend both to the left and right, resulting in "bi-directionality".

From the BERT paper itself:

We note that in the literature the bidirectional Transformer is often referred to as a “Transformer encoder” while the left-context-only version is referred to as a “Transformer decoder” since it can be used for text generation.